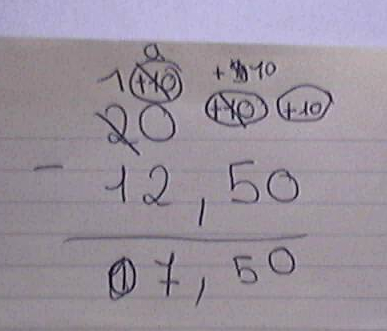La soustraction qui « casse » au CM2 ?

AndréC a écrit:Voici comment la soustraction 20 - 12,5 a été posée et effectuée par cette élève de sixième.

Les ratures font toutes partie intégrante de son calcul, excepté celle du résultat où elle s'est trompée et a corrigé son erreur.

Edit : image en plus grande

Ouh la la :-(

Question annexe : à partir de quel niveau peut-on attendre que (20 - 12,5) se fasse de tête ?

Bouboule a écrit:

Ouh la la :-(

Question annexe : à partir de quel niveau peut-on attendre que (20 - 12,5) se fasse de tête ?

D'autres élèves l'ont fait de tête, pas elle.

Normalement le calcul mental est aussi enseigné à l'école primaire, tel n'a pas été son réflexe.

AndréC a écrit:

Bouboule a écrit:

AndréC a écrit:Voici comment la soustraction 20 - 12,5 a été posée et effectuée par cette élève de sixième.

Les ratures font toutes partie intégrante de son calcul, excepté celle du résultat où elle s'est trompée et a corrigé son erreur.

Edit : image en plus grande

Ouh la la :-(

Question annexe : à partir de quel niveau peut-on attendre que (20 - 12,5) se fasse de tête ?

D'autres élèves l'ont fait de tête, pas elle.

Normalement le calcul mental est aussi enseigné à l'école primaire, tel n'a pas été son réflexe.

Comme il y avait un nombre décimal (certes simple) je me demandais si c'était déjà travaillé en CM2 (ici je suppose qu'on a un cas de la vie courante, je te file un billet de 20 pour payer 12,5).

Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Normalement, cela peut se faire dès l'élémentaire ... si la classe fait régulièrement du calcul mental !!

Je n'avais jamais vu une soustraction comme celle-ci nulle part !
J'ai lu l'autre fil sur le cassage de la dizaine. Dans la méthode classique avec retenue, je trouve trop complexe l'explication liée au fait que la différence entre deux nombres reste inchangée si on ajoute le même nombre aux deux termes de la différence. Les élèves ne comprennent pas le lien avec le fait d'"abaisser la retenue". D'où mon explication personnelle à mes élèves : écrire "1" à côté d'un chiffre du terme inférieur, c'est pour me rappeler que j'ai déjà enlevé une dizaine (ou une centaine) donc je l'écris "en plus" des dizaines (centaines) qu'on devait déjà enlever dans l'opération. Explication qui semble fonctionner, et que je ne trouve pas inexacte.

La méthode de soustraction de Singapour a le même défaut de présentation compliquée que la méthode qui "casse" et barre dès qu'on traite des grands nombres. Pourtant j'utilise Singapour pour la résolution de problèmes (mais je me rends compte que lorsqu'on est seule dans une école à appliquer une méthode, c'est compliqué, surtout quand on essaie de l'introduire en CE2).

AndréC a écrit:Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Et ils devaient calculer 20-12,50... Donc ils avaient l'énoncé et le résultat qu'ils devaient vérifier ?

Maintenant je comprends pourquoi mes terminales soupirent quand je demande de calculer 255-7, "Dites nous combien ça fait et on vous dira si c'est bon."

Verdurette a écrit: Dans la méthode classique avec retenue, je trouve trop complexe l'explication liée au fait que la différence entre deux nombres reste inchangée si on ajoute le même nombre aux deux termes de la différence.  Les élèves ne comprennent pas le lien avec le fait d'"abaisser la retenue".

Je suis entièrement d'accord, c'est trop complexe. Cette technique du cassage donne du sens à la technique opératoire pour les petits nombres. Et c'est très bien.

Ensuite, à mon avis, il faut varier l'explication en leur faisant systématiquement vérifier leur soustraction en posant une addition.

Puis on introduit la technique des retenues sans la justifier autrement que par le constat que cela fonctionne (en posant l'addition).

Cela permet de raisonner par équivalence, c'est à dire que le simple fait que le résultat soit juste permet de valider la technique.
La question de la justification de la technique des retenues ne devant être donnée qu'au final.

Quant à votre technique, je n'ai pas encore eu le temps de la regarder, je vais m'y pencher.

Réflexion de professeur de lettres, que m'inspire cette histoire : à force de vouloir donner du sens aux apprentissages, on en vient à :
- des calculs longs et complexes.
- des élèves qui ont des difficultés à accepter la parole de l'adulte et du professeur si elle n'est pas justifiée scéance tenante.
Contre productif.

Rabelais a écrit:Réflexion de professeur de lettres, que m'inspire cette histoire : à force de vouloir donner du sens aux apprentissages, on en vient à :
- des calculs longs et complexes.
- des élèves qui ont des difficultés à accepter la parole de l'adulte et du professeur si elle n'est pas justifiée scéance tenante.
Contre productif.

Analyse que je partage à 100%. Pédagogisme mortel !

AndréC a écrit:

Bouboule a écrit:Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)

Celle qui est décrite ici : http://mamaitressedecm1.fr/?p=1698

alors là je suis étonné par cette maîtresse du CM1 !

la méthode classique est plutôt :

723
-
697

3 moins 7 : je ne peux pas
donc 13 moins 7 = 6 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU BAS et non en le soustrayant à celui du HAUT

9 +1 (le report) = 10, 2 moins 10 je ne peux pas donc 12 -10 =2 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU BAS
6 +1 (le report) =7
7 - 7 =0
donc 723 - 697 = 026

Je viens de tomber par hasard sur ce message. Je ne comprends absolument rien à la soustraction posée par ton élève Bouboule : que signifie ce charabia ?

Dans les problèmes de monnaie, il est fréquent que l'on utilise la méthode du complément (comme les marchands quand ils rendent la monnaie ) : 12 € 50, et 50 c qui font 13 et 7 euros qui font 20 ...

Sans tout expliciter, comprendre à quoi correspond une retenue, ça me paraît utile ...
Mais je cautionne aussi la vérification de la soustraction !

79 airlines a écrit:

alors là je suis étonné par cette maîtresse du CM1  !

la méthode classique est plutôt :

723
-
697

3 moins 7 : je ne peux pas
donc 13 moins 7 = 6 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU  BAS et non en le soustrayant à celui du HAUT

9 +1 (le report) = 10, 2 moins 10 je ne peux pas donc 12 -10 =2 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU  BAS
6 +1 (le report) =7
7 - 7 =0
donc 723 - 697 = 026

C'est ce qu'elle fait.

On peut faire apprendre une technique aux élèves sans qu'ils aient besoin de la comprendre, et cela peut très bien être à court terme ce qui se fait de plus efficace (en l'occurrence, que les élèves sachent réaliser une soustraction dans le cas le plus général possible). Mais on peut se poser la question de ce que cela induit à plus long terme.

Une image mentale persistante chez de nombreux élèves est qu'en mathématiques il faut appliquer la bonne formule, trouver le bon calcul, bref sortir la boite noire qui opère par magie pour obtenir la solution. Peut-être les élèves ne sont-ils pas prêts pour comprendre tout ce qu'ils font quand ils sont encore dans une phase d'acquisition de technique, mais je crois qu'il est très important de trouver le bon moment pour expliquer ce qui se cache derrière, et que si l'on attend trop (et encore faudrait-il savoir identifier à quel moment a-t-on trop attendu ?), c'est potentiellement très mauvais.

Un exemple qui me vient, et je pense que l'on pourrait en trouver bien d'autres : beaucoup d'élèves/étudiants appliquent la formule du discriminant avec des nombres complexes parce qu'ils ne maitrisent pas le cadre d'usage de la formule, qui est une conséquence directe du fait que l'on ne s'est soucié que de l'apprentissage d'une technique non comprise, avec pour autre illustration le fameux 7=0 de Baruk.

Il me semble que de nombreuses personnes ont déjà eu tout au cours du 20e siècle ce genre de discussion-controverse et qu'elle n'est toujours pas tranchée (et ne le sera sans doute pas dans ce fil...).

Pour en revenir au cas particulier des techniques de soustraction, quelques sources concernant l'apprentissage de l'arithmétique aux USA pendant la première moitié du 20e siècle mentionnent qu'il y avait des différences significatives de pratiques dans plusieurs états, que des gens ont essayé de comparer pour identifier ce qui était le plus efficace, et qu'ils ne sont pas parvenus à un consensus sur la question. Il faut bien avouer toutefois que ce n'est vraiment pas évident à trouver (et j'imagine encore moins à lire...) ; je n'ai jamais pu parcourir que des résumés assez grossiers qui peuvent ne pas donner une idée précise de ce qui a réellement été analysé.

AndréC a écrit:Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Ben ça fait 7,50€ en tout, pas 12,50€, non ? :fifi2:

Ma'am a écrit:

AndréC a écrit:Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Ben ça fait 7,50€ en tout, pas 12,50€, non ? :fifi2:

Je ne l'avais pas précisé, on demande combien le vendeur rend...

jaybe a écrit:
Une image mentale persistante chez de nombreux élèves est qu'en mathématiques il faut appliquer la bonne formule, trouver le bon calcul, bref sortir la boite noire qui opère par magie pour obtenir la solution.

Parce que le plus souvent, c'est vrai, c'est comme cela qu'on leur a appris à faire. Et les élèves sont heureux de faire comme on leur dit de faire car cela paye, cela donne une bonne moyenne.

Lorsque j'étais stagiaire, une collègue stagiaire d'anglais faisait son stage dans le même collège que moi où une collègue de maths, madame T... était très réputé pour être une bonne prof.
Ma collègue stagiaire d'anglais me dit qu'elle l'a eu comme prof en 4e et 3e et me dit textuellement : « Elle est excellente, je comprenais rien et j'avais 15 de moyenne »

Caro a écrit:Je viens de tomber par hasard sur ce message. Je ne comprends absolument rien à la soustraction posée par ton élève Bouboule : que signifie ce charabia ?

Normal, ce n'est pas mon élève

79 airlines a écrit:

AndréC a écrit:

Bouboule a écrit:Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)

Celle qui est décrite ici : http://mamaitressedecm1.fr/?p=1698

alors là je suis étonné par cette maîtresse du CM1  !

la méthode classique est plutôt :

723
-
697

3 moins 7 : je ne peux pas
donc 13 moins 7 = 6 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU  BAS et non en le soustrayant à celui du HAUT

Que nenni!
La méthode classique dit:
— 7 ôté de 3, on ne peut pas. On met une retenue devant le 3 et devant le 9 (certains la mettent dessous, d'autre ajoutent un signe +. Moi, j'ai appris en la mettant  devant (pas longtemps, après, on ne la met plus).
— on fait 7 ôté de 13, cela fait 6.

9 +1 (le report) = 10, 2 moins 10 je ne peux pas donc 12 -10 =2 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU  BAS

— 9 et un de retenue qui fait 10, ôté de de 2, on se remet une retenue (devant le 2 et le 6).
— 10 ôté de 12 fait 2

6 +1 (le report) =7
7 - 7 =0
donc 723 - 697 = 026

— 6 et 1 de retenue fait 7, ôté de 7 fait 0

Donc 723-697=26 (on ne va quand même pas recopier un zéro inutile).

À la place de ôté de on peut dire enlevé à. Mais il faut éviter la tournure descendante avec moins. Les tournures en remontant permettent de réutiliser la retenue tout de suite, ce qui facilite le travail quand on évite d'écrire la retenue.

AndréC a écrit:

Verdurette a écrit: Dans la méthode classique avec retenue, je trouve trop complexe l'explication liée au fait que la différence entre deux nombres reste inchangée si on ajoute le même nombre aux deux termes de la différence.  Les élèves ne comprennent pas le lien avec le fait d'"abaisser la retenue".

Je suis entièrement d'accord, c'est trop complexe. Cette technique du cassage donne du sens à la technique opératoire pour les petits nombres. Et c'est très bien.

Ensuite, à mon avis, il faut varier l'explication en leur faisant systématiquement vérifier leur soustraction en posant une addition.

On ne repose pas l'addition pour vérifier. On la fait de tête en remontant la soustraction posée. La vérification doit être rapide (d'où l'intérêt de la preuve par neuf pour les multiplications et addition).

ycombe a écrit:

AndréC a écrit:

Verdurette a écrit: Dans la méthode classique avec retenue, je trouve trop complexe l'explication liée au fait que la différence entre deux nombres reste inchangée si on ajoute le même nombre aux deux termes de la différence.  Les élèves ne comprennent pas le lien avec le fait d'"abaisser la retenue".

Je suis entièrement d'accord, c'est trop complexe. Cette technique du cassage donne du sens à la technique opératoire pour les petits nombres. Et c'est très bien.

Ensuite, à mon avis, il faut varier l'explication en leur faisant systématiquement vérifier leur soustraction en posant une addition.

On ne repose pas l'addition pour vérifier. On la fait de tête en remontant la soustraction posée.

Vous êtes bien catégorique !

Avez-vous un argument incontestable pour pouvoir affirmer qu'il faut faire exactement comme vous dites et pas autrement ?

AndréC a écrit:

Ma'am a écrit:

AndréC a écrit:Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Ben ça fait 7,50€ en tout, pas 12,50€, non ? :fifi2:

Je ne l'avais pas précisé, on demande combien le vendeur rend...

Justement, on leur rend 12,50e ; c'est 20-7,5 qu'ils doivent calculer, non ?
Par ailleurs je ne comprends pas toujours pourquoi l'enseignante de CM1 de mon fils persistait à vouloir enseigner les soustractions en faisant rayer les nombres en présence pour les remplacer par d'autres lorsque ça coinçait. Avec son système, impossible de vérifier quoi que ce soit, un vrai bonheur. Mais je pense que j'emporterai cette interrogation à l'asile.

RogerMartin a écrit:

AndréC a écrit:

Ma'am a écrit:

AndréC a écrit:Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Ben ça fait 7,50€ en tout, pas 12,50€, non ? :fifi2:

Je ne l'avais pas précisé, on demande combien le vendeur rend...

Justement, on leur rend 12,50e ; c'est 20-7,5 qu'ils doivent calculer, non ?

Oui, en effet, je lui ai fait refaire le problème quelques jours plus tard (entre deux cours) et elle a reposé le problème de mémoire. Je n'ai pas pris la peine de relire l'énoncé, ni elle non plus. L'important était alors de voir la technique en acte.

C'est certainement cela qui lui a fait faire l'erreur au résultat (elle a écrit 1 puis 0).

79 airlines a écrit:

AndréC a écrit:

Bouboule a écrit:Qu'est-ce que vous appelez la technique classique ? Je viens de taper soustraction CM sous google et je m'interroge ;-)

Celle qui est décrite ici : http://mamaitressedecm1.fr/?p=1698

alors là je suis étonné par cette maîtresse du CM1  !

la méthode classique est plutôt :

723
-
697

3 moins 7 : je ne peux pas
donc 13 moins 7 = 6 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU  BAS et non en le soustrayant à celui du HAUT

9 +1 (le report) = 10, 2 moins 10 je ne peux pas donc 12 -10 =2 et je retiens 1 que je reporte en gauche en l'additionnant au chiffre DU  BAS
6 +1 (le report) =7
7 - 7 =0
donc 723 - 697 = 026

Quand on est grand, on fait (723-700)+(700-697)

Ma'am a écrit:La maîtresse de mon fils en CE1 a prévu d'enseigner la méthode de la dizaine cassée et elle nous a plus ou moins interdit de leur montrer la méthode classique à la réunion de rentrée...  

Une maîtresse m'interdirait de faire quelque chose à la maison, Groumph ! Que dirait-elle si je venais plus ou moins lui interdire de montrer certaines méthodes en classe ? Je suppose que le verbe "interdire" est mal choisi, et qu'elle a simplement déconseillé, en le justifiant par la cohérence et la progressivité des apprentissages, n'est-ce pas ? En tout cas, cela me rappelle l'histoire de cette maîtresse de CP qui demandait aux parents de ne pas laisser leurs enfants ouvrir des livres à la maison, parce que cela allait perturber leur apprentissage de la lecture. J'espère que l'histoire est inventée.

Verdurette a écrit:Lorsque je les récupère en CE2, je leur explique qu'ils vont faire des opérations avec des nombres de plus en plus grands.  On ne peut donc plus utiliser cette technique et ils vont apprendre la "technique des grands".  

Ma globule actuellement en CE2 m'a montré la technique suivante (sur une paire de nombre à 3 chiffres au lieu de 4) :
7503 - 4776 :  
7xxx - 4xxx : 3000
Puis : 75xx-47xx : comme 5 est plus petit que 7, on descend de 3000 à 2000, et 15 moins 7 font 8, donc j'en suis à 2800
Puis : 750x-477x : comme 0 est plus petit que 7, on descend de 2800 à 2700, et 10-7 font 3, donc je suis à 2730
Puis : j'enlève encore 6, mais j'ajoute 3, donc je n'enlève que 3, donc je trouve 2727

J'ai trouvé cela très malin de donner l'ordre de grandeur puis de gagner progressivement en précision.

Posé, cela devrait donner quelque chose comme :
'  7503
- 4776
-------
= 3
'  28
'  273
'  2727

RogerMartin a écrit:

AndréC a écrit:

Ma'am a écrit:

AndréC a écrit:Il s'agissait d'un petit problème  où 3 amis consommaient chacun une boisson à 2,50 € pièce. L'un d'eux réglait pour les trois avec un billet de 20 €...

Ben ça fait 7,50€ en tout, pas 12,50€, non ? :fifi2:

Je ne l'avais pas précisé, on demande combien le vendeur rend...

Justement, on leur rend 12,50e ; c'est 20-7,5 qu'ils doivent calculer, non ?
Par ailleurs je ne comprends pas toujours pourquoi l'enseignante de CM1 de mon fils persistait à vouloir enseigner les soustractions en faisant rayer les nombres en présence pour les remplacer par d'autres lorsque ça coinçait. Avec son système, impossible de vérifier quoi que ce soit, un vrai bonheur. Mais je pense que j'emporterai cette interrogation à l'asile.

Ça ressemble à la soustraction des heures, minutes, secondes.

5h34min - 2h56min = 4h94min -2h56min = 2h38min.

Donc en somme, c'est faire en décimal ce qu'on fait en sexagésimal. C'est ça ?